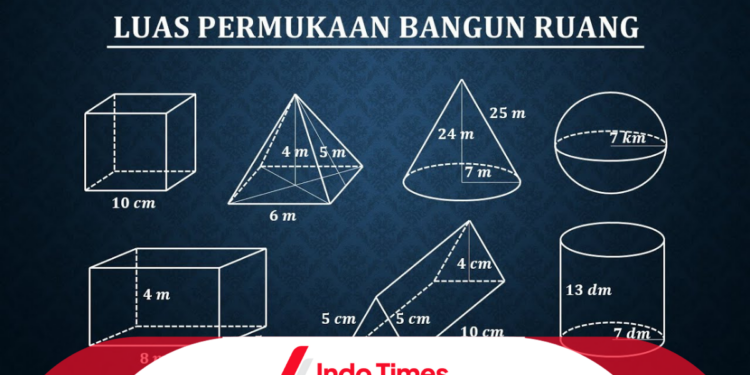
Rumus bangun ruang adalah kunci dalam menghitung berbagai properti geometris dari bangun-bangun tiga dimensi.
Dalam matematika, pemahaman tentang rumus-rumus ini menjadi dasar penting dalam menyelesaikan berbagai permasalahan terkait volume, luas permukaan, atau sifat-sifat lain dari berbagai bangun ruang.
Ada beberapa rumus yang secara konsisten digunakan untuk menghitung properti-properti tersebut, dan pemahaman yang kuat tentang ini dapat mempermudah dalam menyelesaikan masalah matematika yang berkaitan.
8 Rumus Bangun Ruang Beserta Contohnya

Mari kita eksplorasi delapan rumus bangun ruang yang umum digunakan beserta contoh cara menyelesaikan soal menggunakan rumus-rumus tersebut.
Rumus Kubus
Kubus adalah bangun ruang tiga dimensi yang memiliki semua sisi dengan panjang yang sama. Untuk menghitung volume kubus, rumus yang digunakan 3V=s3, di mana s adalah panjang sisi.
Sebagai contoh, jika sisi kubus memiliki panjang 5 cm, maka volumenya kubus adalah =53 =125 cm3.
Rumus Balok
Balok adalah bangun ruang yang memiliki enam sisi, dengan sisi-sisi berlawanan memiliki ukuran yang sama.
Rumus untuk menghitung volume balok adalah V=p×l×t, di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
Misalnya, jika panjang balok adalah 6 cm, lebarnya 4 cm, dan tingginya 3 cm, maka volumenya adalah 6×4×3=72 cm3, V=6×4×3=72 cm3.
Rumus Tabung
Tabung adalah bangun ruang yang memiliki dua lingkaran sejajar sebagai bidang alas dan atasnya. Rumus untuk menghitung volume tabung adalah V=πr2×t.
r adalah jari-jari lingkaran alas, dan t adalah tinggi tabung.
Sebagai contoh, jika jari-jari alas tabung adalah 3 cm dan tingginya 8 cm, maka volumenya adalah π×32×8≈226.2 cm3.
Rumus Bola
Bola adalah bangun ruang tiga dimensi yang bentuknya bulat sempurna. Untuk menghitung volume bola, rumus yang digunakan adalah V=34πr3, di mana r adalah jari-jari bola.
Misalnya, jika jari-jari bola adalah 10 cm, maka volumenya adalah V=34π×103≈ 4188.79 cm3.
Rumus Limas
Limas adalah bangun ruang yang memiliki alas segi-n dengan sisi tegaknya berbentuk segitiga. Rumus untuk menghitung volume limas adalah V=31×luas alas × t.
Luas alas adalah luas alas limas dan t adalah tinggi limas.
Sebagai contoh, jika luas alas limas segitiga adalah 24 cm² dan tingginya 9 cm, maka volumenya adalah V=31×24×9= 72 cm3.
Rumus Prisma
Prisma adalah bangun ruang dengan dua bidang alas yang sejajar dan sisi-sisinya berbentuk segi-n. Rumus untuk menghitung volume prisma adalah V=luas alas × t.
Di mana lua salas adalah luas alas prisma dan t adalah tinggi prisma.
Misalnya, jika luas alas prisma segitiga adalah 30 cm² dan tingginya 6 cm, maka volumenya adalah V=30×6= 180 cm3.
Rumus Kerucut
Kerucut adalah bangun ruang yang memiliki alas lingkaran dan satu sisi lengkung. Rumus bangun ruang untuk menghitung volume kerucut adalah V=31πr2×t.
Di mana r adalah jari-jari lingkaran alas dan t adalah tinggi kerucut.
Sebagai contoh, jika jari-jari alas kerucut adalah 5 cm dan tingginya 12 cm, maka volumenya adalah = 31π × 52 × 12≈ 314.16 cm3.
Rumus Prisma Segitiga Tegak
Prisma segitiga tegak adalah prisma yang alasnya berbentuk segitiga siku-siku. Rumus untuk menghitung volume prisma segitiga tegak adalah V=21 × luas alas × t.
Di mana luas alas adalah luas alas prisma dan t adalah tinggi prisma.
Misalnya, jika luas alas prisma segitiga siku-siku adalah 40 cm² dan tingginya 8 cm, maka volumenya adalah = 21 × 40 × 8 = 160 cm3.
Mengetahui rumus-rumus bangun ruang ini dapat mempermudah dalam menyelesaikan berbagai masalah matematika yang berkaitan dengan bangun-bangun ruang.
Dengan pemahaman yang baik tentang rumus-rumus ini, kita dapat dengan mudah menghitung volume, luas permukaan.
Sifat-sifat lain dari berbagai bangun ruang yang kita temui dalam kehidupan sehari-hari maupun dalam konteks akademis.
Jadi, melalui penerapan rumus-rumus ini, matematika tentang bangun ruang menjadi lebih dapat dipahami dan diaplikasikan secara luas.
Sama halnya dengan memahami rumus simpang kuartil yang bisa Anda terapkan untuk kehidupan sehari-hari.
Fungsi Memahami Rumus Bangun Ruang

Rumus bangun ruang adalah konsep matematis yang memiliki peran penting dalam berbagai aspek kehidupan sehari-hari.
Dalam matematika, rumus-rumus ini digunakan untuk menghitung berbagai properti dan karakteristik dari bangun ruang seperti volume, luas permukaan, serta parameter lainnya.
Meskipun terlihat rumit, aplikasi dari rumus bangun ini dapat dengan mudah dijumpai dalam aktivitas sehari-hari, mulai dari desain arsitektur, teknologi, hingga kegiatan sederhana seperti berbelanja di supermarket.
Dalam dunia arsitektur
Dalam dunia arsitektur dan konstruksi, rumus bangun ruang ini menjadi dasar utama dalam perencanaan dan pembangunan struktur bangunan.
Misalnya, ketika seorang arsitek merancang sebuah gedung, dia harus mempertimbangkan berbagai rumus bangun ini untuk menentukan volume total ruangan, luas permukaan dinding, serta kapasitas ruang tersebut.
Begitu juga dengan seorang insinyur sipil yang membangun jembatan atau jalan raya, mereka harus memanfaatkan rumus bangun ini.
Tujuannya untuk menghitung kekuatan material yang dibutuhkan serta geometri yang tepat agar konstruksi tersebut aman dan kokoh.
Industri teknologi
Tidak hanya dalam bidang teknik, rumus bangun ruang juga berperan penting dalam industri teknologi.
Dalam pembuatan perangkat elektronik seperti ponsel pintar, komputer, dan bahkan kendaraan, penggunaan rumus ini sangat diperlukan.
Sebagai contoh, saat merancang sebuah komponen elektronik yang memiliki bentuk tiga dimensi.
Para insinyur harus menggunakan rumus bangun ruang untuk menghitung volume ruang yang tersedia agar komponen tersebut dapat dipasang dengan tepat tanpa mengganggu fungsi keseluruhan perangkat.
Kegiatan sehari-hari

Penerapan rumus bangun juga dapat ditemui dalam kegiatan sehari-hari yang sederhana seperti berbelanja di supermarket.
Saat membeli barang seperti kotak, botol, atau kemasan lainnya, kita sering kali tidak menyadari bahwa perhitungan volume dari kemasan tersebut didasarkan pada rumus bangun.
Dengan mengetahui volume kemasan, kita dapat memperkirakan berapa banyak barang yang dapat diisi atau berapa banyak ruang yang akan ditempatinya di dalam lemari atau kulkas.
Bidang keuangan dan ekonomi
Selain itu, rumus bangun ruang memiliki peran dalam dunia keuangan dan ekonomi. Dalam perencanaan keuangan, konsep volume dan luas permukaan digunakan untuk menghitung berbagai parameter seperti estimasi pendapatan, keuntungan, dan risiko investasi.
Bahkan, dalam industri perbankan, perhitungan matematis berbasis rumus bangun digunakan untuk menghitung bunga, angsuran, dan berbagai aspek keuangan lainnya.
Dengan demikian, dapat disimpulkan bahwa rumus bangun memiliki peran yang sangat signifikan dalam berbagai aspek kehidupan sehari-hari.
Mulai dari desain bangunan, teknologi, aktivitas konsumen, hingga keuangan, konsep matematika ini memberikan landasan penting bagi banyak bidang dalam menyelesaikan permasalahan dan membuat keputusan yang tepat.
Kemampuan untuk memahami dan menerapkan rumus-rumus bangun ruang dapat memberikan manfaat yang besar bagi individu maupun perkembangan masyarakat secara keseluruhan.
Oleh karena itu, pengertian dan pemanfaatan konsep ini sangatlah penting dalam meningkatkan pemahaman dan kualitas kehidupan kita sehari-hari.